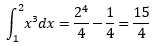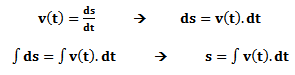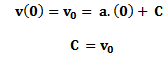Considere uma partícula que se move em linha reta com aceleração dada pela função polinomial a(t) = 6t+ 4 (cm/s²).
a) Encontre a função velocidade sabendo que v(1) = - 6 cm/s.
b) Encontre sua função posição sabendo que s(0) = 9 cm.
c) Determine a variação de posição sofrida pela partícula no intervalo de 1 a 2 segundos.
A resolução dessa situação envolve um processo conhecido como antiderivação ou primitivação: encontrar a antiderivada, ou seja, uma função cuja derivada é conhecida. Assim, dizemos que v(t) é antiderivada de a(t) e s(t) é antiderivada de v(t).
De modo geral, dizemos que F(x) é antiderivada de f(x) sobre um intervalo I se F'(x) = f(x) para todo xI.
No exemplo acima, temos que a(t) = 6t + 4. Para encontrar v(t), pensamos em uma função cuja derivada seja 6t + 4, obtendo, então, 3t² + 4t + C. Como foi dada a informação de que v(1) = - 6, temos:
3.1² + 4.1 + C = - 6
C = - 13
Assim, v(t) = 3t² + 4t - 13.
De maneira similar, obtemos s(t) = t³ + 2t² - 13t + C. E como s(0) = 9, conclui-se que C = 9.
Assim, s(t) = t³ + 2t² - 13t + 9.
Para calcular a variação de posição no intervalo de 1 a 2 segundos, basta calcularmos s(2) - s(1).
s(2) = 2³ + 2.(2)² - 13.2 + 9 = -1 cm
s(1) = 1³ + 2.(1)² - 13.1 + 9 = -1 cm
s(2) - s(1) = -1 - (-1) = 0
Observem que, nessa situação, não precisaríamos ter considerado o valor de C, já que na diferença eles se cancelaram.
Observando o gráfico de s(t) (em preto na figura abaixo) vemos que calcular s(2) - s(1) = B - A = 0 equivale a calcular a seguinte integral definida:
onde s(t) é uma antiderivada de v(t).
De modo geral, se f é contínua em [a, b] e F for qualquer antiderivada de f, então é válido:
Além disso, se permitirmos que o limite de integração superior seja um valor qualquer a ≤ x ≤ b do domínio de f, então a função 
é tal que g'(x) = f(x).
é tal que g'(x) = f(x).
Assim, se quisermos calcular 
podemos tomar uma antiderivada qualquer de x³ (em geral, toma-se a mais simples, ou seja, com C = 0) e avaliá-la nos limites de integração, da forma:
podemos tomar uma antiderivada qualquer de x³ (em geral, toma-se a mais simples, ou seja, com C = 0) e avaliá-la nos limites de integração, da forma:
Utilizamos o símbolo 
para representar a fórmula da antiderivada de f(x). Dessa forma, 
pois 
. A esse processo damos o nome de integração indefinida.
para representar a fórmula da antiderivada de f(x). Dessa forma, 
pois 
. A esse processo damos o nome de integração indefinida.
Uma integral indefinida satisfaz as mesmas propriedades das integrais definidas já trabalhadas anteriormente, a constar:
Note também que, ao calcularmos a variação de posição entre os instantes 1 e 2 segundos na situação inicial apresentada, o que fizemos foi calcular a integral de uma taxa de variação (a velocidade). Assim, a integral de uma taxa de variação F '(x) em um intervalo [a, b] fornece a variação total de F(x) nesse intervalo.
Por exemplo, se v(t) representa o volume de água num reservatório em um instante t e v'(t) é a taxa com a qual a água flui para dentro do reservatório, então:
ou seja, integramos a variação da quantidade de água dentro do intervalo de tempo [a, b].
ESTUDO DO MOVIMENTO RETILÍNEO
Vimos que, para uma partícula em movimento retilíneo, com função posição s(t), sua velocidade e sua aceleração instantâneas são dadas, respectivamente, por:
Desta forma, se conhecemos a aceleração de um objeto em movimento retilíneo, a antiderivação (ou integração) gera uma família de funções velocidade. Do mesmo modo, a antiderivação de v(t) produz uma família de funções posição. Matematicamente, escrevemos:
Manipulando a relação acima, obtemos:
Integrando os dois membros da igualdade, temos:
Da mesma forma, para a velocidade:
Podemos utilizar as relações obtidas para chegar às “fórmulas” trabalhadas e conhecidas nas aulas de física do ensino médio.
Exemplo Consideremos o estudo de um MUV (Movimento Uniformemente Variado). Para essas situações, sabe-se que se tem um movimento em que a aceleração não se altera com o passar do tempo, portanto:
Obtém-se uma família de funções velocidade do tipo 
. Para restringir esta família de funções a uma única função, é necessário se conhecer ao menos um dado de velocidade do objeto ao longo do seu percurso. Se considerarmos que no instante t = 0 a partícula possua uma velocidade arbitrária v0, ou seja, v(0) = v0, temos que:
. Para restringir esta família de funções a uma única função, é necessário se conhecer ao menos um dado de velocidade do objeto ao longo do seu percurso. Se considerarmos que no instante t = 0 a partícula possua uma velocidade arbitrária v0, ou seja, v(0) = v0, temos que:
E, portanto, chegamos à equação geral para a velocidade de um objeto em MUV:
O mesmo procedimento pode ser realizado para obtenção da fórmula geral da posição do objeto ao longo do tempo, utilizando-se o resultado obtido para a velocidade. Temos:
Integrando, obtemos:
Novamente, adotando s(0) = s0 temos:
Obtemos, desta forma, a equação geral para a posição de um objeto que possui movimento uniformemente variado, dada por:
