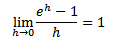Derivada de funções exponenciais
Fonte: GeoGebra Tube
Tomemos 
. Para construir a derivada dessa função:
. Para construir a derivada dessa função:
A quantidade
também é uma constante, embora seu valor dependa de r. Escrevendo k = 
, vemos que a derivada de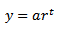 
é proporcional a 
:
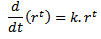
Função exponencial de base "e": o número de Euler
Suponha que queiramos encontrar um valor de r tal que a derivada de f(t) seja exatamente f(t). Isso significa que estamos buscando um valor de r de forma que 
é igual a 1.
Resolvendo para r:
Aplicando o limite em r quando h tende a zero:
Então:
Isso significa que
é a sua própria derivada:
E como consequência sua anti-derivada é:
Fonte: GeoGebra Tube
Autor: Alan Couto
é igual a 1.Resolvendo para r:
Aplicando o limite em r quando h tende a zero:
Esse número é chamado de número de Euler. Possui uma notação própria - um "e" minúsculo e itálico. Sua definição matemática (veja neste texto) lhe garante propriedades muito particulares e importantes e, na maioria das vezes, é usado como base de funções exponenciais para descrever crescimentos/decrescimentos contínuos. Coloque b = 2,7 no gráfico acima e perceba que o gráfico da taxa de variação varia igual sua função original.
Isso significa que
é a sua própria derivada:
E como consequência sua anti-derivada é:
Exemplo 1: aplicação no contexto da derivação
Quando o movimento de um corpo descreve uma trajetória e a partir de certo instante ela começa a se repetir, dizemos que esse movimento é periódico. Alguns exemplos são o sistema massa-mola e o pêndulo de um relógio, quando um desses conjuntos descrevem um "vai e vem" em torno de suas posições de equilíbrio. Devido às forças de dissipação, como o atrito, os movimentos reais, em geral, possuem uma duração finita. Nesse caso, dizemos que seu movimento é amortecido. Um caso particular desse tipo de movimento é aquele em que o deslocamento num tempo t é descrito pela função 
, que derivando, obtemos:
, que derivando, obtemos:
Essa função é definida para todo número real, uma vez que 
é diferente de 0 para todo t. Igualando essa derivada a 0, encontramos que a função original tem pontos críticos quando sent = - cost, ou, de forma equivalente, quando tg(t) = -1, pois:
é diferente de 0 para todo t. Igualando essa derivada a 0, encontramos que a função original tem pontos críticos quando sent = - cost, ou, de forma equivalente, quando tg(t) = -1, pois:
sent = - cost
sent/cost = -1
tg(t) = -1
Essa equação tem infinitas soluções uma vez que:
t = -3π/4 + kπ, para todo k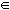 
Z (inteiro relativos)
Z (inteiro relativos)
Como 
, o resultado são as oscilações permanecerem, atingindo seus máximos e mínimos para t = -3π/4 + kπ, para todo k Z, porém com sua amplitude diminuindo ao longo do tempo t. No gráfico abaixo você pode manipular os parâmetros da função, conforme a lei:
, o resultado são as oscilações permanecerem, atingindo seus máximos e mínimos para t = -3π/4 + kπ, para todo k Z, porém com sua amplitude diminuindo ao longo do tempo t. No gráfico abaixo você pode manipular os parâmetros da função, conforme a lei:
Exemplo 2: integração por substituição simples.
Exemplo 3: uma nova técnica de integração - quando a substituição simples não se aplica.
Questões para estudo deste conteúdo
